例一:高斯判别分析和logistic函数
我们来看一个例子,对于一个高斯判别分析问题,根据贝叶斯:
$$
\begin{align}
p(y=1|x) &= \frac{p(x|y=1)p(y=1)}{p(x)} \\
&= \frac{p(x|y=1)p(y=1)}{p(x|y=0)p(y=0)+p(x|y=1)p(y=1)}
\end{align}
$$
在这里,我们提出几个假设:
- $p(y)$是均匀分布的,也就是$p(y=1)=p(y=0)$
- $x$的条件概率分布($p(x|y=0)$和$p(x|y=1)$)满足高斯分布。
考虑二维的情况:
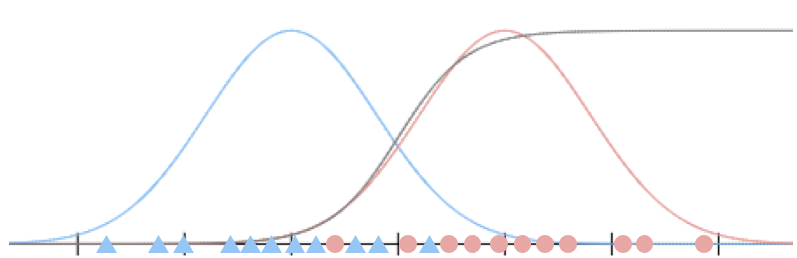
蓝色数据表达的是$p(x|y=0)$的分布,红色数据表达的是$p(x|y=1)$的分布,两条蓝色和红色的曲线分别是它们的概率密度曲线。
而灰色的曲线则表示了$p(y=1|x)$的概率密度曲线。
假设$p(x|y=0) \sim N(\mu_0, \sigma_0)$,$p(x|y=1) \sim N(\mu_1, \sigma_1)$,而$p(y)$均匀分布那么:
$$
\begin{align}
p(y=1|x) &= \frac{N(\mu_0,\sigma_0)}{N(\mu_0,\sigma_0)+N(\mu_1,\sigma_1)} \\
&= \cdots \\
&= \frac{1}{1+\frac{\sigma_0}{\sigma_1}exp(2\sigma_1^2(x-\mu_0)^2-2\sigma_0^2(x-\mu_1)^2}
\end{align}
$$
事实上,这条曲线跟我们之前见过的logistic曲线非常像,特别是当我们假设$\sigma_0=\sigma_1$的时候,就是一条logistic曲线。
我们有如下的推广结论:
$$
{\begin{cases}
p(x|y=1) \sim Exp Family(\eta_1) \\
p(x|y=0) \sim Exp Family(\eta_0)
\end{cases}} \Rightarrow p(y=1|x)是logistic函数
$$
但这个命题的逆命题并不成立,故而我们知道,logistic所需要的假设更少(无需假设$x$的条件概率分布),鲁棒性更强。而生成函数因为对数据的分布做出了假设,所以需要的数据量会少于logstic回归,我们需要在两者之间进行权衡。
例二:垃圾邮件分类(1)
这里我们会用朴素贝叶斯(Naive Bayes)来解决垃圾邮件分类问题($y\in \lbrace 0, 1 \rbrace$)。
首先对邮件进行建模,生成特征向量如下:
$$
x=
\begin{bmatrix}
0 \\
0 \\
0 \\
\vdots \\
1 \\
\vdots
\end{bmatrix}
\begin{matrix}
a \\
advark \\
ausworth \\
\vdots \\
buy \\
\vdots
\end{matrix}
$$
这是一个类似于词频向量的特征向量,我们有一个50000个词的词典,如果邮件中出现了某个词汇,那么其在向量中对应的位置就会被标记为1,否则为0。
我们的目标是获取,垃圾邮件和非垃圾邮件的特征分别是怎么样的,也即$p(x|y)$。$x={\lbrace 0, 1 \rbrace}^n, y \in \lbrace 0, 1 \rbrace$,这里我们的词典中词汇数量是50000,所以$n=50000$,特征向量$x$会有$2^{50000}$种可能,需要$2^{50000}-1$个参数。
我们假设$x_i|y$之间相互独立(虽然假设各个单词的出现概率相互独立不是很合理,但是即便这样,朴素贝叶斯的效果依旧不错),根据朴素贝叶斯,我们得到:
$$
p(x_1, x_2, \ldots, x_{50000}|y)=p(x_1|y)p(x_2|y) \cdots p(x_{50000}|y)
$$
单独观察$p(x_j|y=1)$:
$$
p(x_j|y=1) = p(x_j=1|y=1)^{x_j}p(x_j=0|y=1)^{1-x_j}
$$
给定三个参数:
$$
\begin{align}
\phi_{j|y=1} &= p(x_j=1|y=1) \\
\phi_{j|y=0} &= p(x_j=1|y=0) \\
\phi_y &= p(y = 1)
\end{align}
$$
故:
$$
\begin{align}
p(x_j|y=1) &= \phi_{j|y=1}^{x_j}(\phi_y - \phi_{j|y=1})^{1-x_j}\\
p(x_j|y=0) &= \phi_{j|y=0}^{x_j}(1-\phi_y + \phi_{j|y=0})^{1-x_j} \\
p(x_j|y) &= p(x_j|y=1)^yp(x_j|y=0)^{1-y} \\
p(y) &= \phi_y^y(1-\phi_y)^{1-y}
\end{align}
$$
按照上个博客8. 生成学习算法的概念中所述,我们会选用联合概率分布的极大似然来导出最优解:
$$
l(\phi_y,\phi_{j|y=1},\phi_{j|y=0}=\prod_{i=1}^mp(x^{(i)},y^{(i)})=\prod_{i=1}^mp(x^{(i)}|y^{(i)})p(y^{(i)})
$$
可以解得:
$$
\begin{align}
\phi_{j|y=1} &= \frac{\sum_{i=1}^m1\lbrace x_j{(i)}=1, y^{(i)}=1 \rbrace}{\sum_{i=1}^m1\lbrace y^{(i)}=1 \rbrace} = \frac{统计所有包含词语j的垃圾邮件的数量}{垃圾邮件的总数}\\
\phi_{j|y=0} &= \frac{\sum_{i=1}^m1\lbrace x_j{(i)}=1, y^{(i)}=0 \rbrace}{\sum_{i=1}^m1\lbrace y^{(i)}=0 \rbrace} = \frac{统计所有包含词语j的非垃圾邮件的数量}{非垃圾邮件的总数} \\
\phi_y &= \frac{\sum_{i=1}^m1\lbrace y^{(i)}=1 \rbrace}{m} = \frac{垃圾邮件的数量}{邮件的总数}
\end{align}
$$
通过以上的公式,我们已经可以完全推得$p(x_1, x_2, \ldots, x_{50000}|y)$。
Laplace平滑
假设,训练集中,我们重来没有碰到过”NIPS“这个词汇,假设我们词典中包含这个词,位置是30000,也就是说:
$$
\begin{align}
p(x_{30000}=1|y=1) &= 0\\
p(x_{30000}=0|y=1) &= 0
\end{align} \\
\Downarrow \\
p(x|y=1) =\prod_{i=1}^{50000}p(x_i|y=1)=0 \\
p(x|y=0) =\prod_{i=1}^{50000}p(x_i|y=0)=0
$$
故而在分类垃圾邮件时:
$$
\begin{align}
p(y=1|x) &= \frac{p(x|y=1)p(y=1)}{p(x)} \\
&=\frac{p(x|y=1)p(y=1)}{p(x|y=0)p(y=0)+p(x|y=1)p(y=1)} \\
&= \frac{0}{0+0}
\end{align}
$$
所以,我们提出$p(x_{30000}=1|y=1) = 0$这样的假设不够好。
Laplace平滑就是来帮助解决这个问题的。
举例而言,在计算:
$$
\phi_y=p(y=1)=\frac{\text{numof(1)}}{\text{numof(0)}+\text{numof(1)}}
$$
其中,$\text{numof(1)}$表示的是,被分类为1的训练集中数据个数。
在Laplace平滑中,我们会采取如下策略:
$$
\phi_y=p(y=1)=\frac{\text{numof(1)}+1}{\text{numof(0)}+1+\text{numof(1)}+1}
$$
比如,A球队在之前的五场比赛里面都输了,我们预测下一场比赛赢的概率:
$$
p(y=1)=\frac{0+1}{0+1+5+1}=\frac{1}{7}
$$
而不是简单的认为(没有Laplace平滑)是0。
推广而言,在多分类问题中,$y\in\lbrace1, \ldots, k \rbrace$,那么:
$$
p(y=j) = \frac{\sum_{i=1}^m1\lbrace y^{(i)} = j \rbrace+1}{m+k}
$$
例三:垃圾邮件分类(2)
之前的垃圾分类模型里面,我们对邮件提取的特征向量是:
$$
x=[1,0,0,\ldots,1,\ldots]^T
$$
这种模型,我们称之为多元伯努利事件模型(Multivariate Bernoulli Event Model)。
现在,我们换一种特征向量提取方式,将邮件的特征向量表示为:
$$
x=[x_1,x_2,\ldots,x_j,\ldots]^T
$$
$x_j$表示词汇$j$在邮件中出现的次数。上述的特征向量也就是词频向量了。这种模型,我们称为多项式事件模型(Multinomial Event Model)。
对联合概率分布$p(x,y)$进行极大似然估计,得到如下的参数:
$$
\begin{align}
\phi_{k|y=1} &= p(x_j=k|y=1) = \frac{C_{x=k}+1}{C_{y=1}+n} \\
\phi_{k|y=0} &=p(x_j=k|y=0) = \frac{C_{x=k}+1}{C_{y=0}+n} \\
\phi_{y} &= p(y=1) = \frac{C_{y=1}+1}{C_{y=1}+1+C_{y=0}+1}
\end{align}
$$
其中:
$n$表示词典中词汇的数量,也就是特征向量的长度;
$$
C_{x=k}=\sum_{i=1}^m(1\lbrace y^{(i)}=1 \rbrace \sum_{j=1}^{n_i}1 \lbrace x_j^{(i)} = k \rbrace)
$$
表示在训练集中,所有垃圾邮件中词汇$k$出现的次数(并不是邮件的次数,而是词汇的次数);
$$
C_{y=1}=\sum_{i=1}^n(1\lbrace y^{(i)} = 1 \rbrace \cdot n_i)
$$
表示训练集中垃圾邮件的所有词汇总长;
$$
C_{y=0}=\sum_{i=1}^n(1\lbrace y^{(i)} = 0 \rbrace \cdot n_i)
$$
表示训练集中非垃圾邮件的所有词汇总长;