翻译自论文:Wavelet-based Visual Analysis of Dynamic Networks,2017 TVCG
图的傅里叶变换
Graph Fourier Transform
关于傅里叶变换请看:【转】傅里叶分析之掐死教程(完整版)
关于拉普拉斯矩阵的一些特性可以看我的另一篇博客:拉普拉斯矩阵二分法
假设一个无向正权图$G=(V,E)$,其邻接矩阵表示成$A$,每个元素代表边的权重。其度矩阵表示成$D$,是一个对角矩阵,对角线的元素则是每个节点所带的连接边的权重和($d_{ij}=\sum_kw_{ik}$),这里不考虑自环。那么拉普拉斯矩阵(Laplacian)就是$L=D-A$。
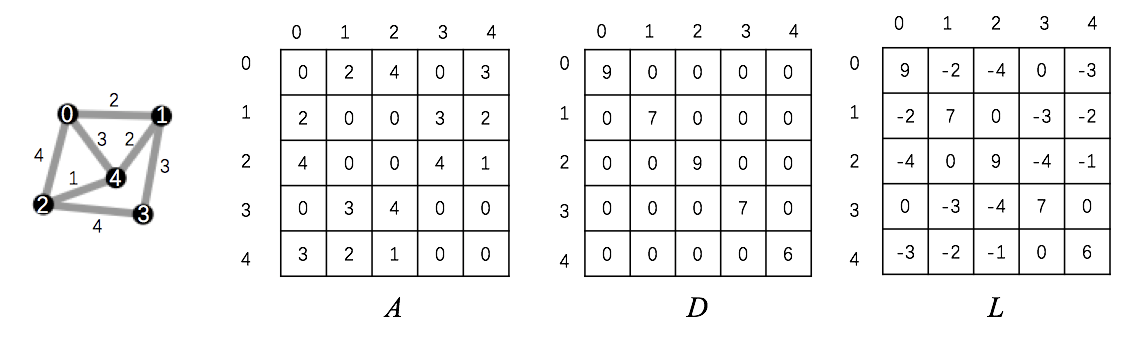
拉普拉斯矩阵是对称的半正定矩阵。因此有一组标准正交的特征向量${u_i}, i \in {1,…,n}$,对应一组递增的非负实特征值${\lambda_i},i \in {1,…n},0=\lambda_1<\lambda_2\leq\cdots\leq\lambda_n$。小的$\lambda_i$就对应了傅里叶变换中的低频。
假如给定一个将节点$V$映射成实数$\Bbb R$的实函数$f$,那么在频率$\lambda_l$上,$f$对应的傅里叶变换可以定义成:
$$
\hat{f}(l)=u_l^T \cdot f = \sum_{j=1}^n u_l(j)f(j)
$$
其中,$u_l(j)$是特征向量$u_l$中$j$位置的值,$f(j)$则是节点$j$的函数值。
对比原连续傅里叶变换从时域转换成频域:
$$
F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt
$$
那么图的傅里叶变换就是从节点转换成对应的拉普拉斯矩阵特征值上。
谱图小波变换
Spectral Graph Wavelet Transform
小波变换参考:形象易懂讲解算法I——小波变换
Hammond于2011年提出了这个概念:Wavelets on graphs via spectral graph theory。
图的小波变换公式:
$$
W_f(s,j)=\sum_{l=1}^ng(s\lambda_l)\hat f(l)u_l(j)
$$
上述的公式中,$j$还是代表了节点,在解释$s$之前,我们来说明一下函数$g$:
$$
g(x) = \begin{cases}
x^2, &\text{for $x < 1$} \\
-5+11x-6x^2+x^3, &\text{for $1\leq x \leq 2$}\\
4x^{-2}, &\text{for $2 < x$}
\end{cases}
$$
函数形状为:
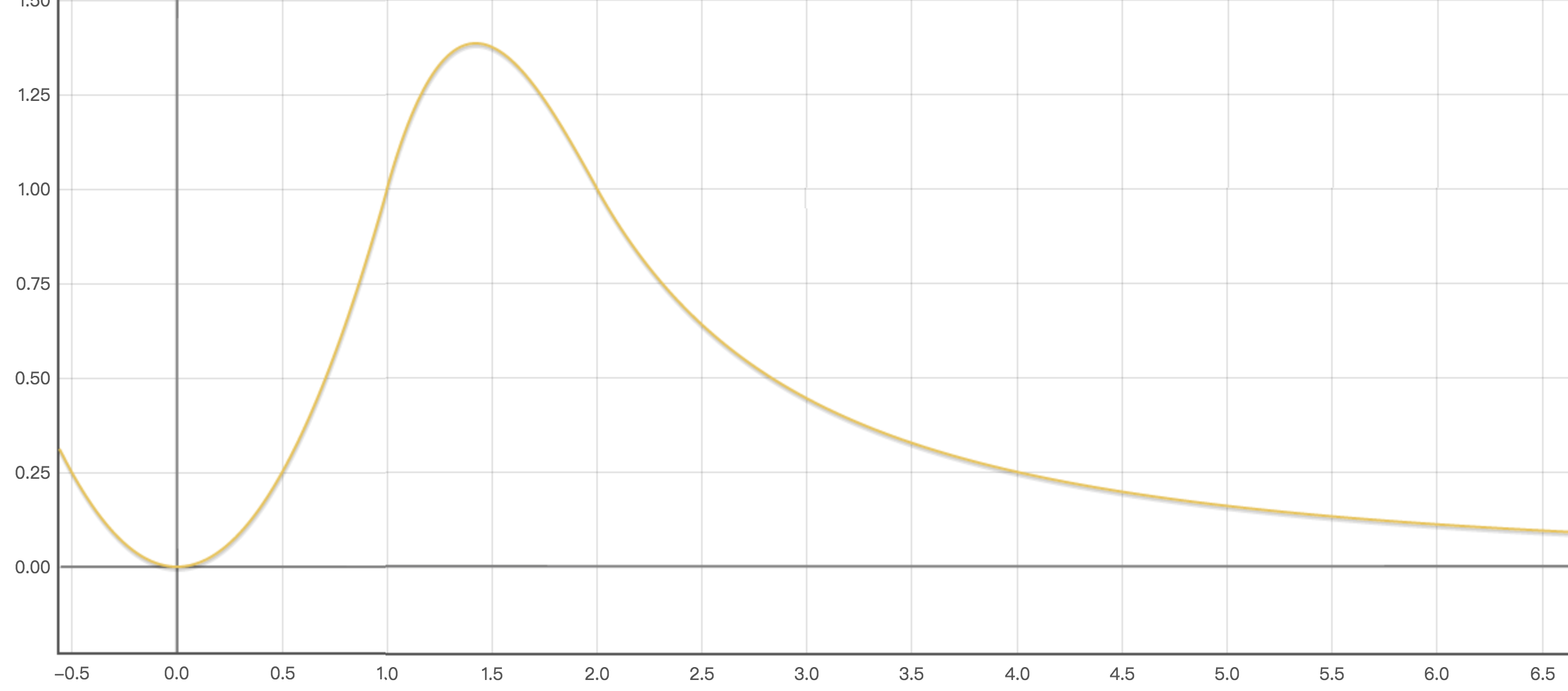
可以得知,当$x$在$[1,2]$之间时,$g(x)$会较大。所以小的$s$值,会对大的$\lambda_l$(对局部特征描述的更详细)更有效果,而大的$s$则对小的(也就是低频的)$\lambda_l$(粗糙的描述了节点的局部特征)更有效果。
我们知道,傅里叶变换仅仅将时域转换成频域,但无法知道特定时间的频域(因为它没有时间维度);小波变换解决的问题就是能够知道特定时间上的频域是如何的,见形象易懂讲解算法I——小波变换。
以此类比:
图的傅里叶变换中,我们将整个图转换成到了特征值上,用不同特征值的权重来表达了整张图,但无法对每个节点生成其特征值分布。
而通过小波变换,可以获取每个节点上,不同$s$值的分布,也就代表了特征值的分布。
特征值能够描述图的特性,比如特征值中0的个数表达了图中连通子图的数量,第二小的非零特征值可以用来描述二分最小切割边数量(代数连通度,algebraic connectivity,见另一篇博客拉普拉斯矩阵和代数连通度)。
小的特征值(对应大的$s$)对全局的描述更强一些,大的特征值则对局部的描述更详细一些。
通过对$s$的值进行采样,我们可以得到一组$s_{min}=s_1,s_2,\ldots,s_r=s_{max}$,一般会取$s_{min}=2/\lambda_n, s_{max}=40/\lambda_n$,对应的$g(sx)$则被称为小波核(wavelet kernels),生成的$W_f(s, j)$则被称为小波系数(wavelet coefficients)。
缩放函数 Scaling function
缩放函数($h(x)$)可以用来生成缩放函数系数($S_f(j)$)是一种用来稳定的表达低频的傅里叶模式(Fourier modes,也就是相对较小的特征值)的方法。一般会跟上述的小波变换产生的wavelet coefficients,$W_f(s_1, j), W_f(s_2, j), \ldots, W_f(s_r,j)$组合,当成wavelet coeffients,其中这个缩放函数(scaling function)则用于表达低频的傅里叶模式:${S_f(j), W_f(s_r, j), \ldots, W_f(s_1,j)}$
这个缩放函数系数$S_f(j)$:
$$
S_f(j)=\sum_{l=1}^nh(\lambda_l)\hat{f}(l)u_l(j)
$$
其中,缩放函数:
$$
h(x)=\gamma exp(-(\frac{10x}{0.3\lambda_n})^4)
$$
小波系数的解释
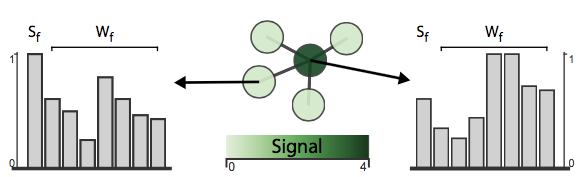
小波系数可以解释成在特定频率的原始信号的能量。传统的小波变换中,高频区域对邻域的表达更好一些,所以相邻点之间在高频区域会有较大的差别,但在低频区域的差别更平滑。在网络(或者说图)中,也是一样的。
图的小波变换,能够为每个节点生成一组系数,代表了不同频率的能量。如下图所示,小波变换系数的分布更为平滑的节点,往往是低频节点(指的是低频率的小波系数更为突出的节点,图中浅绿色的节点),而反之,则是高频节点(高频系数更为突出,图中深绿色节点),小波系数分布不是很平滑,相邻的小波系数之间差距可能会较大。