布局方法
节点链接法
树状布局
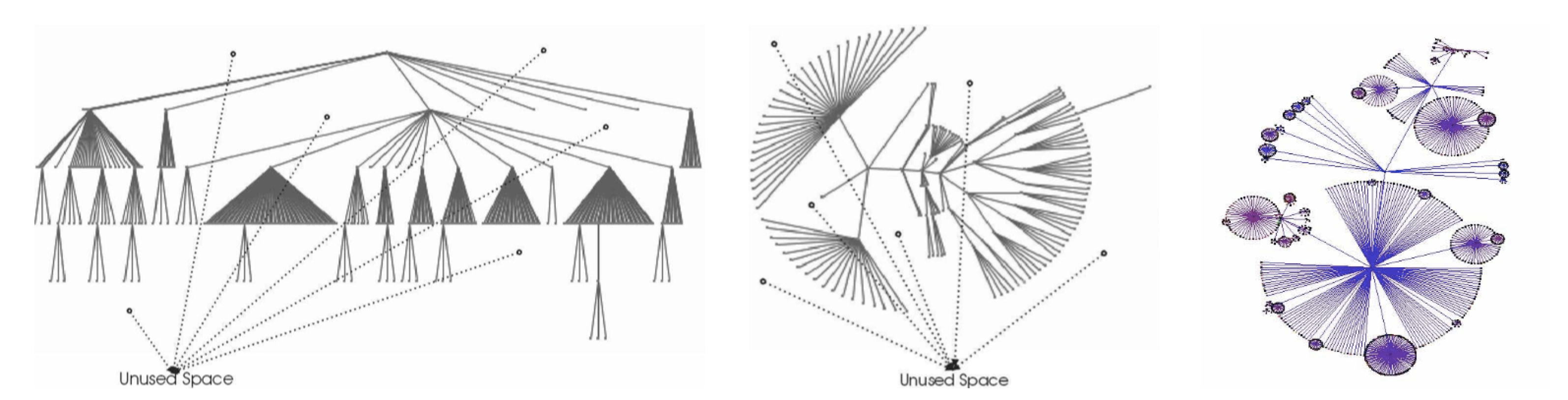
三种不同方法:经典树状布局、径向布局、气泡布局,它们的相关发展:
- 经典
- 1981年,Tidier Drawings of Trees),提出了一种较美的树图,但是空间利用率低。
- A Compact Explorer For Complex Hierarchies将树的分支进行部分重叠以压缩大图,但是会损失信息
- Compact layout of layered trees提出了一种不用把父节点放中间的方法
- 径向
- Radial layout(Eades’s algorithm)A parent-centered radial layout algorithm for interactive graph visualization and animation and variations
- 气泡
- Ballon layoutInteracting with Huge Hierarchies: Beyond Cone Trees
树+链接布局
- Munzner的方法适合可视化最小生成树。
- TreePlus
- 最常见的方法:找到最小生成树,然后用经典树布局、径向树布局、treemap等进行可视化,并且把剩余的边加回来。
弹簧布局
- Newton-Raphson method:Automatic Display of Network Structures for HumanUnderstanding.
- simulated annealing method: Drawing graphs nicely using simulated annealing.
- GEM method: A Fast Adaptive Layout Algorithm for Undi-rected Graphs.
- 可以用来解决一些节点重叠的问题:
- Layout Adjustment and the MentalMap.,水平和垂直方向进行扫描,看看有没有重叠的点,然后迭代的移到不重叠的位置
- Using spring algorithms to remove node overlapping.,
- 力引导布局,单次迭代时间是$O(n^2 + m)$,n是节点数,m是边数,一般需要迭代$O(n)$次达到一个理想的布局,时间复杂度经常是$O(n^3)$,甚至$O(n^4)$,而且同一个算法,同一个数据跑出来经常是不同的两个布局
空间分割布局(Space Division Layout)

- 包含父子关系和兄弟关系。
- 上图(Focus+Context Display and Navigation Techniques for Enhancing Radial, Space-Filling Hierarchy Visualizations)是一个centre-out布局,空间利用率高,但是节点的大小很难控制,实际上有很多节点的节点也会变得很大,空间浪费
空间嵌套布局(Space Nested Layout)
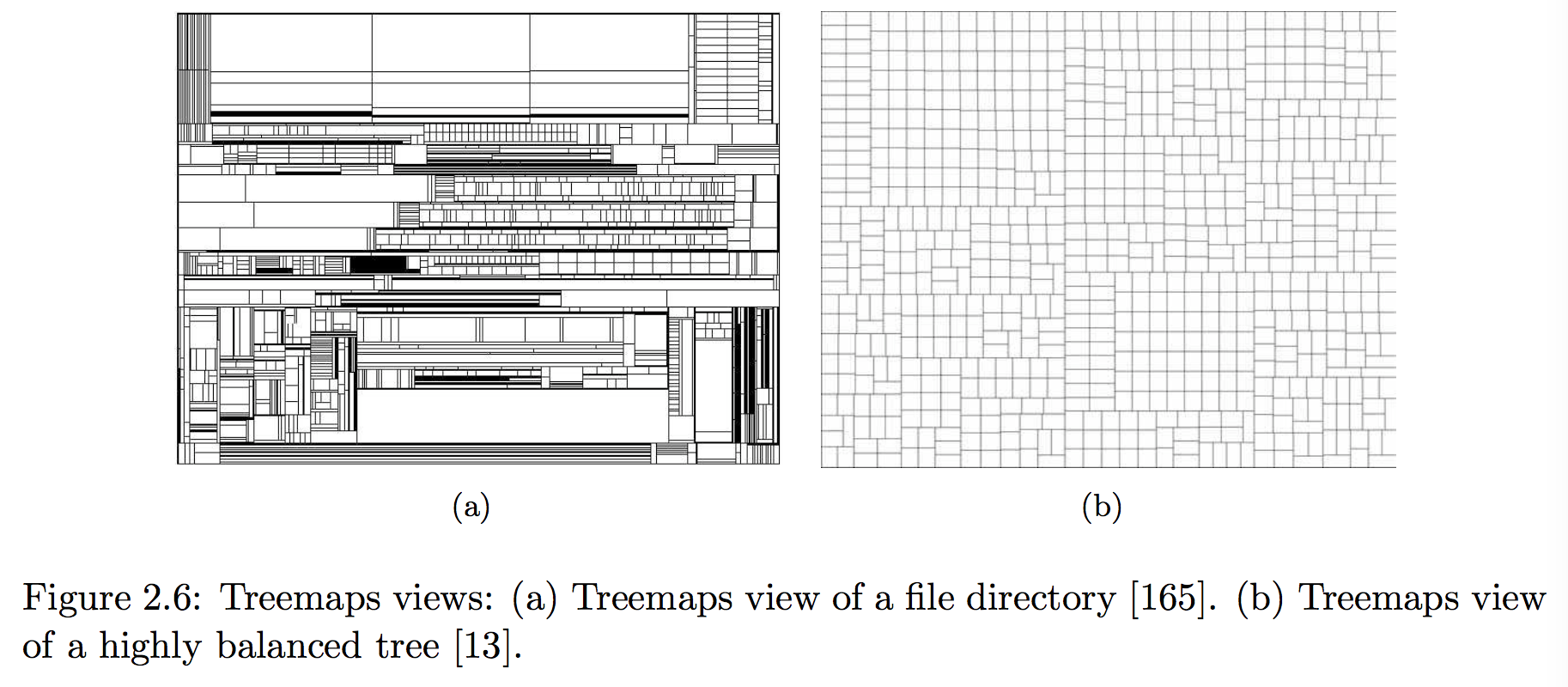
- 最具代表性的:treemap,也有圆形的,circle packing(Visualization of Large Hierarchical Data by Circle Packing ),几个缺点:
- 很容易出现很细的矩形,导致交互问题
- 跟树状布局一比,层次结构比较难分辨
- 容易误导,相邻的两个矩形,在数据中不一定相近
矩阵布局
NodeTrix和MatLink,矩阵和节点连接图的结合

Matrix Zoom: A Visual Interface to Semi-external Graphs用层次聚合方法来对大的矩阵进行可视化和导航(聚合树)
图可视化技术
降低视觉杂乱
三种方法:边位移、点聚类、采样。
边位移
直接优化:直接优化边的交叉是一个NP问题。有一些妥协的用来降低边交叉的方法:
- Simple and Efficient Bilayer Cross Counting设计了一个二分图的边交叉减少的算法
- Overlaying Graph Links on Treemaps用一种非对称曲线,使得treepmap中的曲线向source方向偏移的方法,来提高辨识度
- Applying crossing reduction strategies to layered compound graphs提出了一种用来降低分层复合图的边交叉的方法。
- Two new heuristics for two-sided bipartite graph drawings提出了两个启发性的用以降低二部图的边交叉的策略
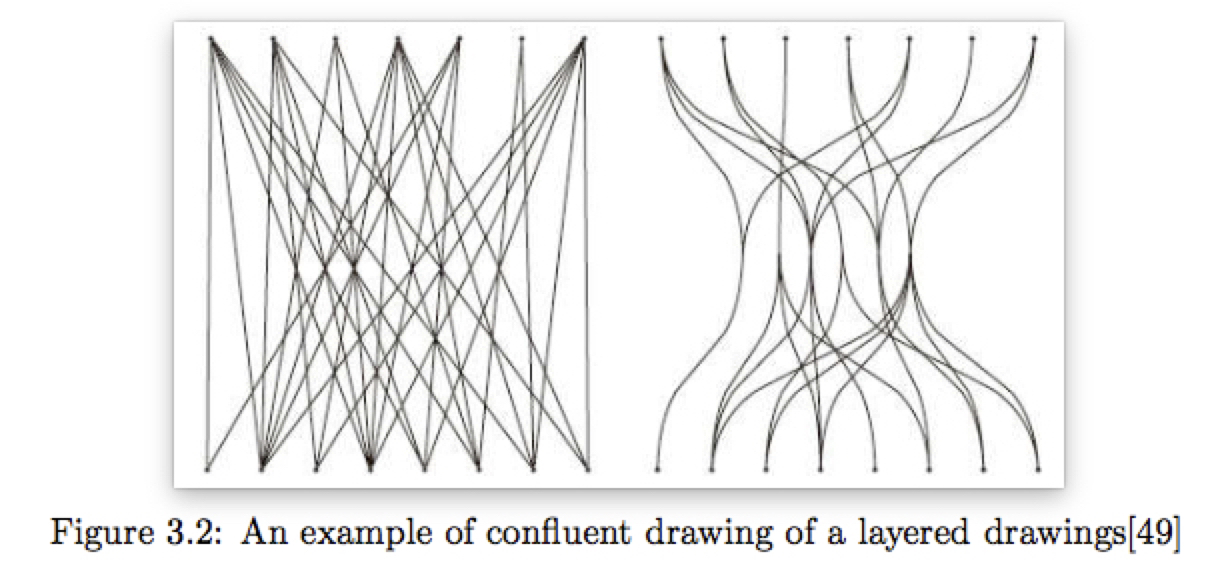
合流绘制:Confluent Layered Drawings并不是直接降低边交叉,而是用曲线来使得边交叉部分变得平滑。基本思想是在交叉的地方,将边捆绑在一起,两个点只能通过平滑曲线才能相连。
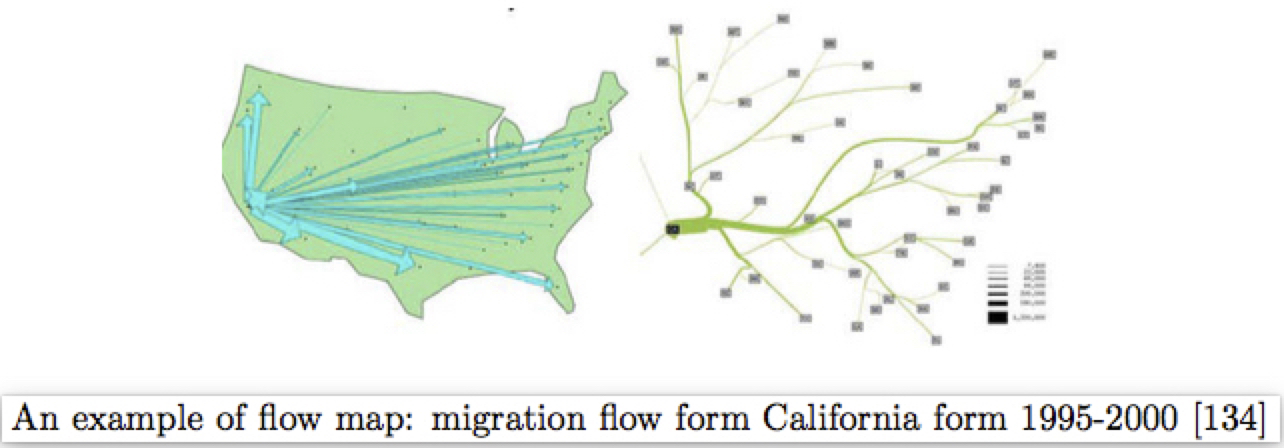
边聚类(Edge clustering):Flow Map Layout 提出一种生成flow map布局的算法,但是只能应用于一组有共同端点边,然后把它们换成二叉树布局:
边捆绑(Edge bundles):关注于tree+link布局,如果两条边共享一个tree path,那么它们就会被聚合在一起。

边扭曲的方法,使得能空出一部分空间。
- EdgeLens:在视野点将边进行扭曲,而不改变点的位置。
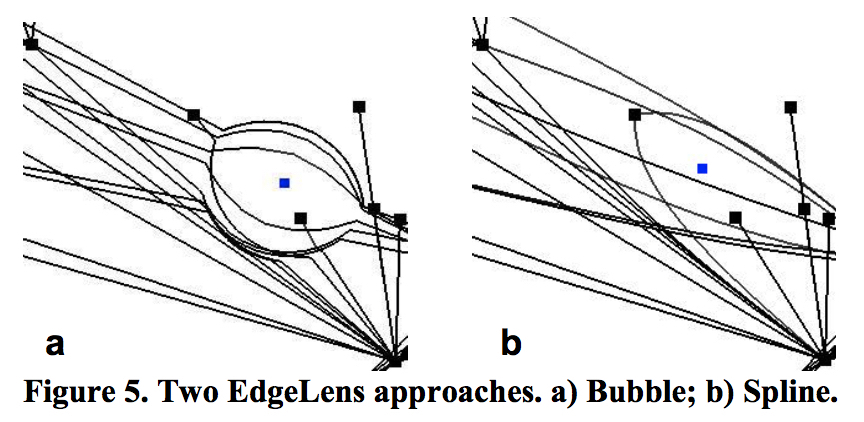
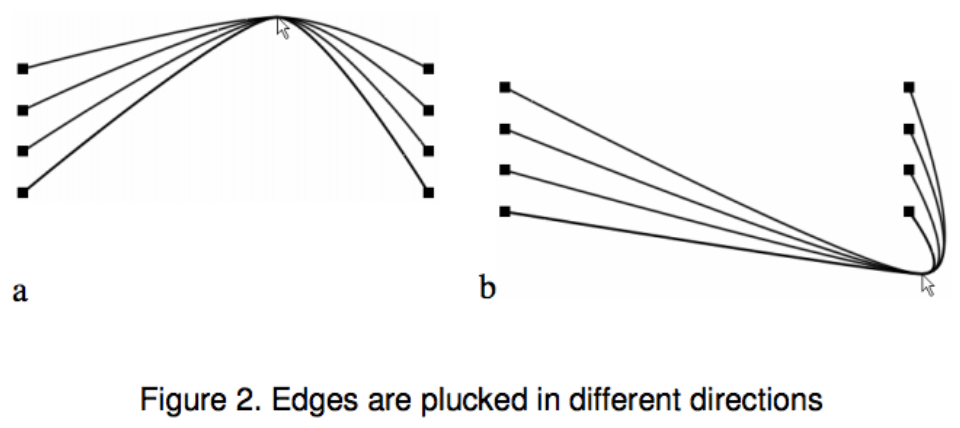
Edge Plucking:像百叶窗一样拉扯
点聚类
聚类的意义是将整个图分割成几个小的子图。有很多种不同的技术,它们主要的区别是,点与点之间距离的定义或者是相似度的定义,有两类不同的定义方法:
- 基于内容的(content-based),用图中元素的语义信息来进行聚类。但是基于内容的方法,依赖于对应的应用场景,不具备太多的通用性。
- 基于结构的(structure-based),会将内部边比外部边更密集的一部分点,聚类为一个聚类。三类方法:
- Graph Theoretical:基于相似度矩阵,spectral bisection,spectral quadrisection and octasection,multilevel spectral bisection
- Single-pass:通过往一个初始节点上加入新节点,形成足够大的聚类。graph growing,greedy cluster
- Iterative algorithms:使用其他聚类算法产生的聚类,作为起点,将小的聚类合成大的聚类,所以是一种层次聚类的方法(hierarchical)。三个主要步骤:
- coarsening graph:粗粒度化
- partitioning graph:切割
- projecting and refining graph:投影和提炼
时间复杂度是节点聚类算法的另一大难题,找到最优聚类仍然是一个NP问题,经典的启发式聚类算法graph growing-1970需要$O(m^2n)$的时间复杂度。Newman的快速聚类算法要$O((m+n)n)$的时间复杂度。
- Balanced cluster:每个聚类的大小应该差不多,分布应该均匀
- Small cluster depth:聚类层次深度应该较浅
- Convex cluster drawings:每一个聚类的绘制都应该是一个简单凸区域
- Balanced aspect ratio:每个聚类区域不要太瘦
- Efficiency:高效的计算和绘制效率
- Symmetry:最大化对称性
采样
- 随机采样:最普遍的方法,Rafiei和Curial在Effectively Visualizing Large Networks Through Sampling中阐述了多种基于采样的方法,显示在大多数情况下,在采样之后,网络的拓扑属性可以被保留下来。引入了“focus”的概念,来加入人的决策以提升采样结果。对focus区域和非focus区域权重不一。
- 随机采样具有不可预测性,于是:
- Measuring data abstraction quality in multiresolution visualizations提出了两种方法(Histogram Difference Measure and Nearest Neighbor Measure.)来测量数据的抽象质量以判断采样策略是否优质。
- Sampling from large graphs比较了已有的采样算法,给出了两种不同的采样目标:the back-in-time goal(采样后的图S要和原始图G在S的尺寸下相似) and the scale-down goal(要尽可能保留原始图的属性)
交互和导航
基于交互的目的,可以分成七类:
- 选择:帮助用户高亮特定目标,或者让计算机去处理一些特定的项目
- 探索:它用于将当前视图点跟改为相同布局表示中的另一部分数据,比如平移和旋转
- 再配置:用于在相同表示方案(矩阵形式、节点链接形式等)的不同布局(力引导布局、树状布局等)之间进行切换,比如替换图中的节点,以及根据不同的标准重新排列数据
编码:它用于切换不同的表示方案,例如将布局从节点链接形式更改为轮廓表示**
抽象/具象:它调整数据表示的抽象级别,为用户提供对数据的不同见解,例如缩放和聚类
- 过滤:它可以减少显示的数据量,并根据用户的要求使剩余的内容更具可读性
- 连接:它用于突出显示与焦点相关的内容,或者内容之间的连接。
其中,探索,抽象/具象,以及过滤,这三个方法最有效。
缩放与平移
基本介绍:
缩放和平移是探索大图的基础方法。平移意味着平稳移动观察点,而缩放则能让用户在数据的抽象或具象视图之间切换。这两个方法互为补充,都不可或缺。
进阶
语义缩放( zooming):意味着当用户放大或缩小时,信息内容会随之发生变化。当用户放大到特定区域时,会显示更多详细信息,当用户缩小时,隐藏详细信息,只显示抽象信息。
问题
当用户在观察地图的时候,可能它们已经放大到了杭州地区,但是此时用户想查看深圳的细节,通常需要将地图缩小,平移到深圳,再进行放大。中间的这些放大缩小的步骤,和用户想要的目标并不相关,但缺少这些步骤,显然需要更长的时间才能找到深圳。此外,用户必须在不同的缩放级别下,用户还需要调整自己的认知,以便在不同的缩放级别下识别同一个项目。
- 解决:SPACE-SCALE DIAGRAIVIS: UNDERSTANDING MULTISCALE INTERFACES提出空间尺度图的概念,通过堆叠不同放大级别的原始二维表示的副本,来构造一个抽象空间,于是各种缩放和平移操作,可以描述为这个堆叠空间中的路径。例如,平移的交互操作指的是相同层中的路径,而缩放操作则是从一个层到另一个层的路径。
过滤
基本介绍:过滤是指从视图中隐藏或强调部分内容。
多种方法:
动态查询过滤器:查询参数可以通过滑块,按钮等快速调整。这些原则的关键在于利用人类视觉信息处理的巨大能力来帮助快速过滤观看项目。
LensBar:LensBar-Visualization for Browsing and Filtering Large Lists of Data一个由Masui提出的接口工具,提供了另一种简化过滤过程的思路。浏览和查询的操作都集成在LensBar中变成一个简单的滚动滑块,用户可以通过关键词过滤来控制显示的数据量。
Magic Lenses:Toolglass and Magic Lenses: The See-Through Interface也提供了一种简化过滤过程的思路。用户可以在显示界面上移动Magic lens,无论移动到何处,它覆盖的区域将显示对应的信息。改进:sampling lens,采样透镜,用于显示覆盖区域的采样结果,见下图:

解释性语言:GUESS: a language and interface for graph exploration.提出了用解释性语言来帮助探索性任务,而不是点击或者滚动。通过将解释语言与图形前端相结合,用户可以通过键入命令来过滤和浏览图结构
焦点+上下文
基本介绍:焦点+上下文技术,常见特点是,它们都允许用户能够放大一个或者多个特定部分,而不会丢失在整个数据集中的位置。
方法:
非失真方法:
- 老方法:用不同的分辨率,在不同区域分别显示。
- Powers of Ten Thousand: Navigating in Large Information Spaces将概览放在与焦点相同的空间中。通过使概览层和焦点层半透明地进行堆叠,用户可以同时在同一个显示中看到它们。
失真的方法:
通过结构的扭曲,实现类似鱼眼镜头的方法,GRAPHICAL FISHEYE VIEWS OF GRAPHS

The Generalized Detail-In-Context Problem:扩展和推广了鱼眼技术,这种拓展不仅仅提供了不同级别进行失真的手段(例如,替换掉带有图标的节点)还构建了对应的未失真图像的其他版本的图像(例如,为鱼眼扭曲提供附加的颜色描述)
Topological fisheye views for visualizing largegraphs:提出了另一种大规模图的拓扑鱼眼的方法。他们的鱼眼显示了一个焦点,其周围具有完整的详细网络,离焦点越来越远的节点,分辨率越来越粗糙。
缺点
- 鱼眼技术会扭曲整个图像,甚至是感兴趣的区域
- 有时候图形硬件不能很好地支持这种失真效果
动画
动画最重要的功能就是帮助用户了解数据集,因为它隐含地将时间作为额外的维度来帮助挖掘数据。
- Cone Trees: animated 3D visualizations of hierarchical information认为,动画可以帮助用户减少思考,因为它将部分认知任务转移到人类的视觉系统。与不同视图之间直接转换相比,动画转换可以更好地提供关于数据关系的线索,并帮助用户关联系统的两个状态。
- 过度使用动画,会使用户分心。Animation: can it facilitate的研究表示,只要静态的表示是直观清晰的,那么即便数据包含了时间维度,使用静态的布局也是一个不错的选择。
- 动画会过度消耗时间,为了实现运动的平滑性,每秒10帧通常被认为是最小所需帧速率。
图可视化的任务
根据Network Visualization by Semantic Substrates和Graph Signatures for Visual Analytics定义了以下几种任务:
- 对于整个图,统计节点数量
- 对于给定节点,统计它的边数
- 对于给定节点,统计它的邻接节点
- 对于一个给定节点,找到可以在一定步数内找到的点或者某一种路径
- 对于整个图,找到中间人节点
- 对于整个图,找到强连接集合
- 对于整个图,找到共享某些特定属性的所有节点链接