Structure-aware Fisheye Views for Efficient Large Graph Exploration

image-20181116171253691

  • 论文原标题： Structure-aware Fisheye Views for Efficient Large Graph Exploration

一、介绍

图对于描述关系数据很通用，已经应用于很多领域，复杂的图的布局会有视觉混乱。

交互则是用于减轻这个问题的通用方法之一。包括，平移缩放（pan-and-zoom）配合概览+细节（overview+detail）技术。介绍了概览细节技术的缺点，有可能会打破有趣的结构，比如长路径，聚类或者一些中等规模的结构（空间连续性问题）。

可更换的技术是：焦点上下文技术（focus+context）。最常见的就是鱼眼，能够放大感兴趣区域。

鱼眼技术的缺点。基于几何的鱼眼技术，比如图鱼眼（graphical）双曲线浏览（ hyperbolic browser）在缩放的时候会忽视图的结构从而带来畸变。拓扑鱼眼寻求解决这个问题（通过coarsen graph得到图的hierarchy，从而保留图结构的方法），然而这个方法并不一定通用。其他还有一些方法并没有通过放大来增加可读性，而是通过一些比如防止节点重叠的方法。但这种方法不支持缩放。一些将链接渲染成曲线的方法则会阻碍图探索。

文章推出了一套框架，可以产生结构相关的鱼眼。其可视化设计由Cohe导出：

  1. 最小化结构的扭曲；
  2. 提升感兴趣区域的可读性；
  3. 在交互的时候要维护连续性。

文章的关键技术是将鱼眼的缩放问题转化成一个优化问题，目标是通过保留边的方向，从而提供可交互的，光滑的，跟结构相关的缩放。如此，文章提出的方法就可以最小化局部结构的扭曲从而提升空间连续性。并且，通过引入美学限制（比如最小化节点重合）来提升图布局的可读性。还有，文章的方法允许用户交互式的（通过画圈，或者画一个层次结构）在鱼眼交互的时候来指定保留特定的结构。

另一方面，作者设计了一个任务导向的鱼眼透镜：

  1. 多焦点透镜：在多个焦点附近高亮结构
  2. 聚类透镜：可以维持一个子结构
  3. 路径透镜：可以聚焦到一个用户指定的路径上

文章的方法基于GPU，能够支持最多15K的节点数量。并且定量的跟以前的方法进行了比较。

贡献：

  1. 提出了一个统一的框架，能够生成用于探索大图的结构相关的鱼眼视图。
  2. 设计了一组任务导向的鱼眼透镜，适用于不同的可视化任务。
  3. 利用基于GPU的方法进行实现，并进行了一次评估，一个user study，以及两个case study。

二、相关工作

图探索技术

pan-and-zoom，fisheye views，semantic zooming，dynamic layout

高质量图布局技术

stress-based methods：将几何限制转换成优化问题。早期的工作专注于方向的限制。但是这个优化问题往往是NP问题。Dig-CoLa方法则有效的解决了有限制的布局的优化问题，通过将限制集成为压力优化（stress majorization）。

三、背景

图$\lbrace V, E\rbrace​$，节点的位置：$X=\lbrace x_1, \cdots, x_n \rbrace​$，其中$x_i \in R^2​$。

几何鱼眼

graphical fisheye，hyperbolic fisheye，iSphere

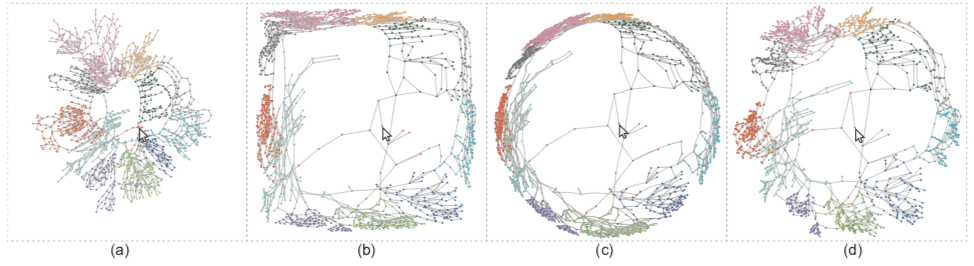
上述的鱼眼基本都是跟几何变换相关，但是忽视了边的链接。会造成结构的扭曲，如封面图b和c。

Edge Vector-based Stress Majorization（布局方面）

$$
arg\min_X\sum_{i<j}w_{ij}(x_i-x_j-e_{ij}d_{ij})^2
$$

e为边的目标方向，d为边的目标长度。在这种布局方法的启发下，作者期望通过改变边的朝向跟长度，来产生一个结构相关的并且能够光滑过渡的鱼眼交互。

四、结构相关的鱼眼（structure-aware fisheye）

$$
arg\min_{Z^t}\sum_{(i, j) \in E} \omega_{ij}^s||z_i^t-z_j^t-e_{ij}^sd_{ij}^s||^2 \\
+\sum_{(i, j) \in \Omega} \omega_{ij}^r||z_i^t-z_j^t-e_{ij}^rd_{ij}^r||^2 \\
+\sum_{i \in \lbrace 1\ldots n \rbrace} \omega_i^t||z_i^t-z_i^{t-1}||^2 \\
$$

其中，$Z^t$指第t次迭代的节点位置，$\omega_{ij}^s, \omega_{ij}^r, \omega_i^t$是归一化的权重，$\Omega$是在焦点区域内的边的集合。$e_{ij}^s$和$d_{ij}^s$则提供了结构的限制，$e_{ij}^r$和$d_{ij}^r$则提供了可读性的限制。最后一项则表达了时序上的连续性也就是光滑过渡。

值得注意的是，$\Omega$并不只是那些可见的边，其包含了所以点对之间的关系，即便两个点之间没有边相连，因为需要使没有边相连的点相互远离。

结构相关的限制

$$
e_{ij}^s=\frac{x_i-x_j}{||x_i-x_j||}, d_{ij}^s=||x’_i-x’_j||
$$

$X’$表示的是用鱼眼透镜估计的目标位置。保持了方向的一致性。

形状限制：上述的限制只保证了边方向的限制，只会让局部结构保持的比较好，而较大的结构会被扭曲，如下图，a是初始图，b是经过graphical fisheye的产出，c是加入了边方向限制，d则是加入了形状限制。

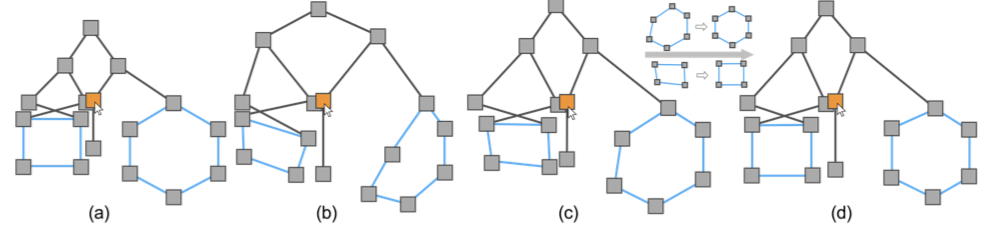
image-20181116171318315

为了保留初始的结构，文章需要用户提供一组连接的边，称为$E_s$，比如上图c中的其中一圈蓝边，那么算法就能更好的估计$d_{ij}^s$。在缩放的时候，有些边变长，有些边变短。我们需要平衡这种变换。
$$
\min_{\rho} \sum_{(i, j) \in E_s}(\rho d_{ij}-d’_{ij})^2
$$
这里估计出了一个平均畸变率$\rho$，使得上图c产生的结构的边长$d’$和$\rho d_{ij}$之间的差距最少。

由此可以计算得到这个畸变率，那么对所有边长都乘上这个畸变率，就能进行统一变换，再加上上面的边方向的保持，从而保持原结构。

$$
d_{ij}^s=\rho d_{ij}
$$

可读性限制

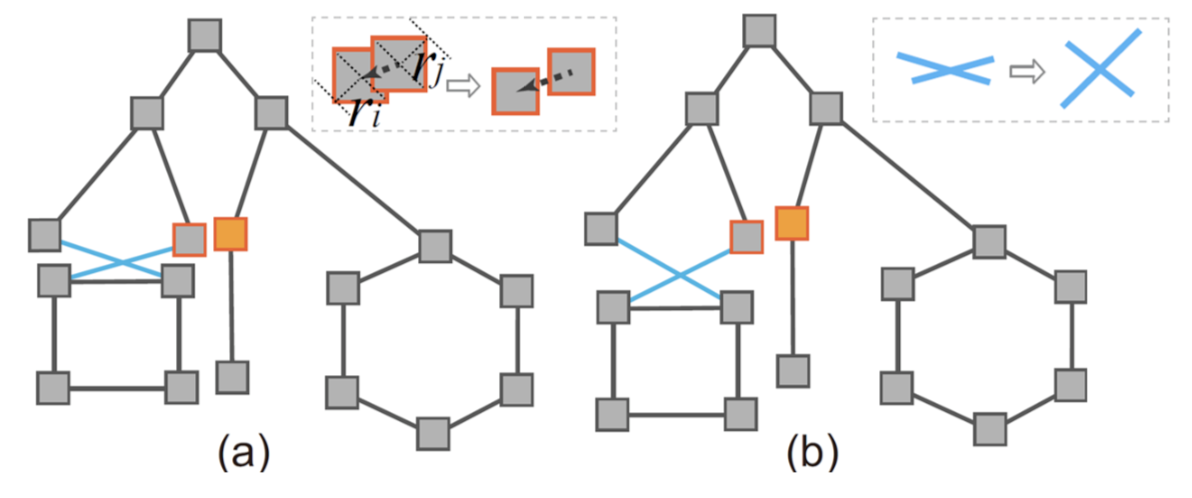
不重叠的节点：
$$
d_{ij}^r=r_i+r_j+\varepsilon, e_{ij}^r=e_{ij}^s
$$
$r_i$和$r_j$是节点包围盒的半径，$\varepsilon$则是节点分离系数（设为屏幕尺寸的1%）。当然这中间还包括了那些不出现的虚拟边（也就是没有相连的两个节点之间也要分离）

最大化边的夹角：

Purchase的可读性研究证明，边的相交很能影响可读性。完全解决边相交的问题不可能，特别是大图。最近的研究表明最大化夹角能够提升路径追踪任务的能力。
$$
e_{ij}^r=e_{ij}^s\oplus\frac{\pi - \alpha}{2}, e_{lk}^r=e_{lk}^s\ominus\frac{\pi - \alpha}{2}
$$
其中$\alpha$是两条边的夹角，$\oplus$表示顺时针旋转，$\ominus$表示逆时针旋转。

五、任务导向的鱼眼透镜

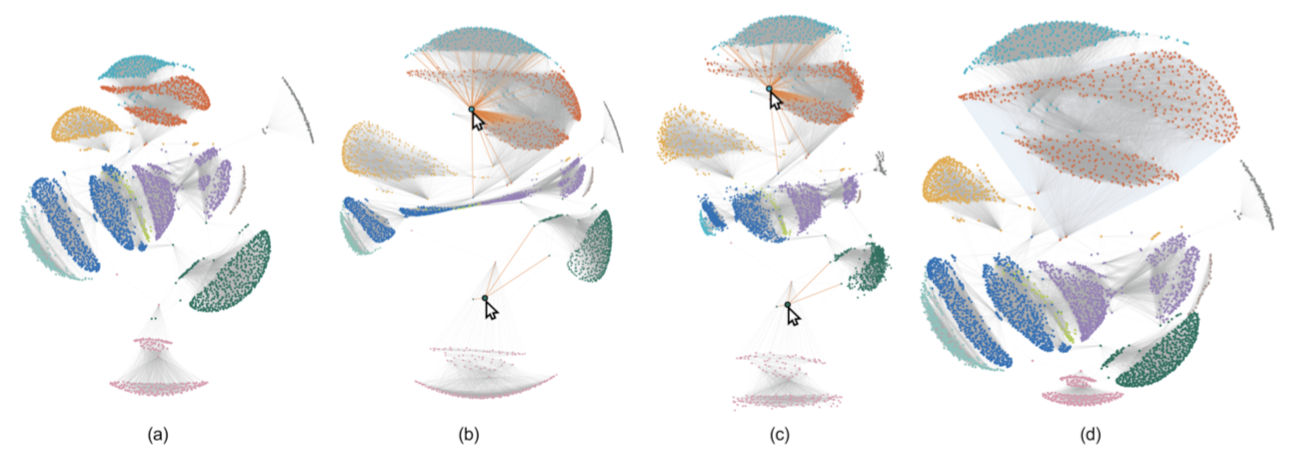
多焦点透镜：在上面的基础上，加入了多焦点的透镜，效果如下图c，b是对照组。

聚类透镜：用户可以制定一个凸包从而可以放大该区域包含的聚类，如图d，红色的聚类是放大聚类，用灰色背景高亮起来。

路径透镜：用户简单的挑选两个节点，算法找到最短路径，然后沿着这条路径定义焦点区域，关于这个焦点区域的半径：屏幕尺寸的$\sqrt{m}/28$，其中$m$是放大系数。

六、结果和评估

定量比较

对照组：

  • graphical fisheye(GF, M. Sarkar and M. H. Brown. Graphical fisheye views of graphs. In Proc. SIGCHI conference on Human Factors in Computing Systems, pp. 83–91, 1992. doi: 10.1145/142750.142763)

  • hyperbolic fisheye(HF, T. Munzner. Exploring large graphs in 3d hyperbolic space. IEEE Computer Graphics and Applications, 18(4):18–23, 1998. doi: 10.1109/38.689657)

  • iSphere(F. Du, N. Cao, Y.-R. Lin, P. Xu, and H. Tong. isphere: Focus+ context sphere visualization for interactive large graph exploration. In Proc.SIGCHI conference on Human Factors in Computing Systems, pp. 2916–2927, 2017. doi: 10.1145/3025453.3025628)

考虑因素：

  • 边方向保留
  • 节点重叠
  • 形状保留

其中，比较双曲线鱼眼的时候，用了iSphere这篇文章的实现来进行比较，而iSphere在放大之后会把非焦聚区域放在球体的背面，无法比较前两项指标。

一共比较了六组方法：GF HF ISphere以及GF+ours，HF+ours，ISphere+ours。前面三者都是直接变换，而后面三者则是一个优化问题。

边方向保留：用Edge Orientation Offset(EOO)，边方向偏差来定义边方向偏差。
$$
EOO(Z)=1-\frac{1}{|E|}\sum_{(i,j) \in E}||\langle \frac{x_i-x_j}{||x_i-x_j||}, \frac{z_i-z_j}{||z_i-z_j||} \rangle||
$$
也就是：1-所有边的初始矢量和变换后的边矢量之间的绝对内积（夹角的cos值的绝对值）的平均值。即EOO越小，边方向保留的越好。

这里只考虑了边方向的变化，而未考虑边长度。它也就揭示了结构的保存完好程度。

下图a表示了EOO，三种应用了文章方法的技术表现明显优于未应用的。

节点不重叠：比较了初始输入跟输出之间的节点重叠数量的差别。下图b表示了重叠的节点的数量，能看到文章的方法效果不错。

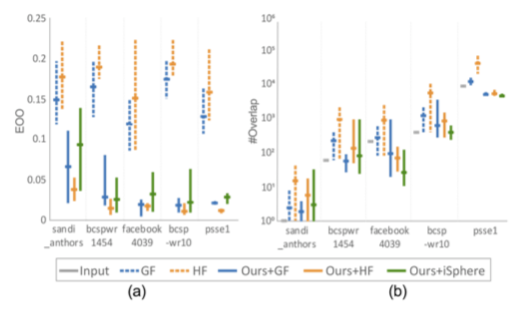
image-20181116171403266

形状保留：利用Eades提出的基于形状的美学指标。给定一组节点组成一个图，将该组节点的k最近邻的集合构成的图叫做它的shape graph。那么，通过mean Jaccard similarity来比较缩放前后，某个图的shape graph的相似度，就可以看出其是否保留形状。

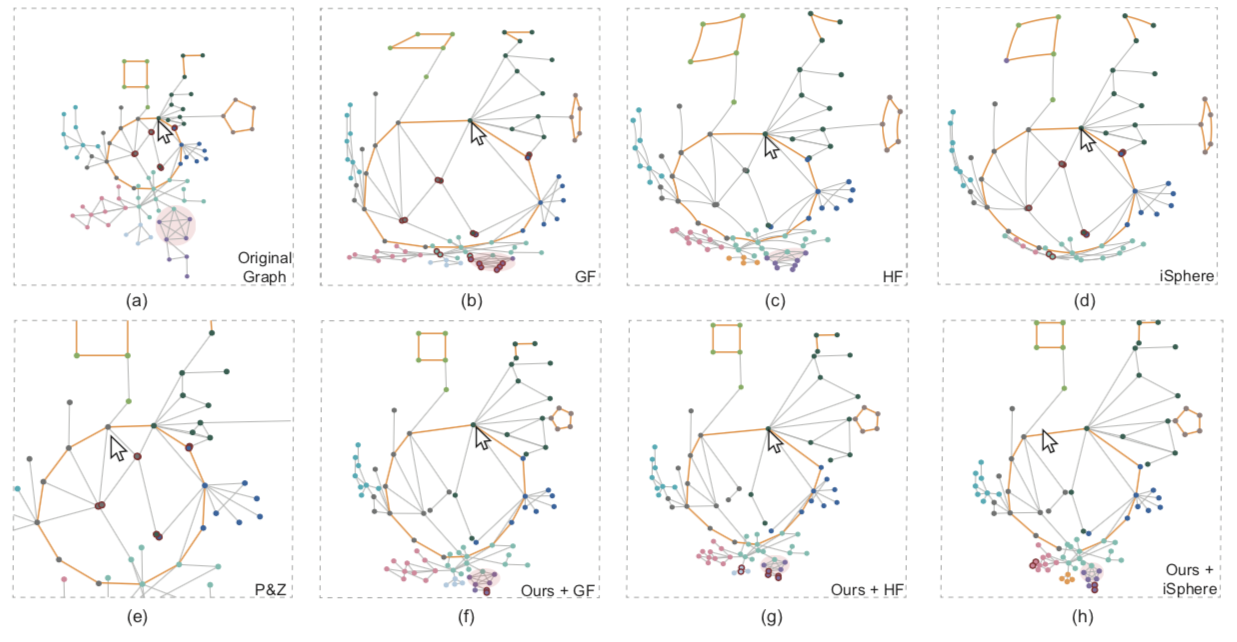
下图展示了不同的透镜下的结果（初始布局是利用一个限制了某些形状的，并且聚类之间不重叠的限制的压力模型），a是初始图，b是graphical fisheye，c是hyperbolic fisheye，d是iShpere，e是线性放大，f是文章方法结合graphical fisheye，g是文章方法结合hyperbolic fisheye，h是文章方法结合iSphere。

Lab Stydy

为了验证文章的structure-aware fisheye是否能够有效提升图探索效率，文章设计了这个lab study。比较了五个技术：

  • pan-and-zoom(P&Z)
  • graphical fisheye(GF)
  • hyperbolic fisheye(HF)
  • iSphere
  • 文章方法+graphical fisheye(Ours+GF)，因为这个表现适中，没有很好也不是很坏。

因为传统的方法并没有考虑可读性的限制，于是在这里只是用了边方向限制作为比较。

实验条件

任务：DU在iSphere这篇文章中已经做过节点、边、路径探索的实验了，而本文的方法保持了边的方向，明显可以在探索节点和边的时候表现更好，并且这一点已经被pivot实验确认了。故而本文的任务聚焦到一个对探索大规模图的比较重要的“路径探索”上。这里主要采用了Xu在A user study on curved edges in graph visualization中使用的找到两个随机选择的节点之间的最短路径的方法。根据pivot实验，这个任务太复杂，于是限制最短路径的长度应该在3-5之间。

数据集：图规模和聚类结构是两个影响用户表现的主要因素。聚类结构可以通过模块度（modularity）来进行度量，越高说明聚类越清晰。因为iSphere证明了在小图下，前面几种方法差别不大。并且在大规模图，低、高模块度的情况下，iSphere都能表现的更好，而HF则表现的明显更差。作者根据iShpere的方法生成哼了1024节点0.6模块度的图作为数据集。并且选取了3作为平均节点度数，这样使得任务不会太难。然后用stress majorization来产生最初布局。在这个数据集中，作者与计算了725个节点对，其中90%的最短路径小于5。

系统实现：系统界面支持选择机制来帮助用户探索，用户右击节点，高亮该节点和连接边。

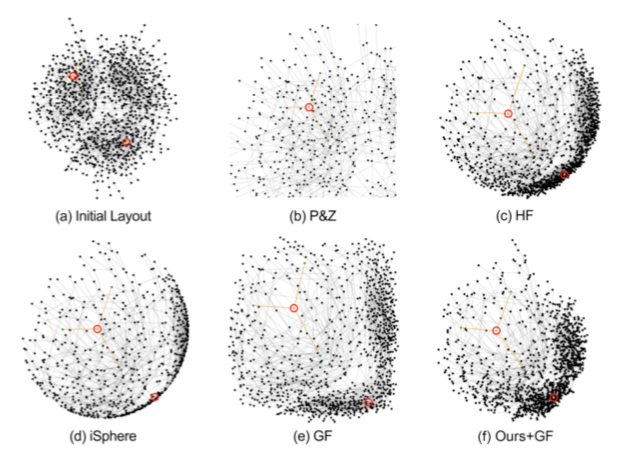
参与者跟设施：40名，24男16女，22-29岁（平均24岁），实验放在桌面电脑上进行，有鼠标键盘，24寸显示器1920 1080分辨率，144hz刷新率（真有钱）。节点连接图白色背景，节点为一个黑点，边则是黑线，而窗口大小则是150mm 150mm。下图是初始布局和五种不同技术放大后的效果。

过程：在一开始，为参与者介绍五种技术。然后会有两条练习来熟悉五种技术：跟正式测试一样，也是找到两个随机选择的节点之间的最短变。

之后每个人要经过15条测试（每个技术3条）。15条测试以及5种技术都是随机的以防止偏见。每个trial都有60s时间限制。每个人大概会花15分钟。

假设：

  1. 用直线渲染的技术（GF, P&Z, Ours+GF）会比曲线（HF，iSphere）来的高效。
  2. 鱼眼技术（GF，HF，iSphere和Ours+GF）则会比没有context的技术（P&Z）更高效。
  3. 低畸变率（Ours+GF，P&Z）会比高畸变率（GF，HF，iSphere）更高效。

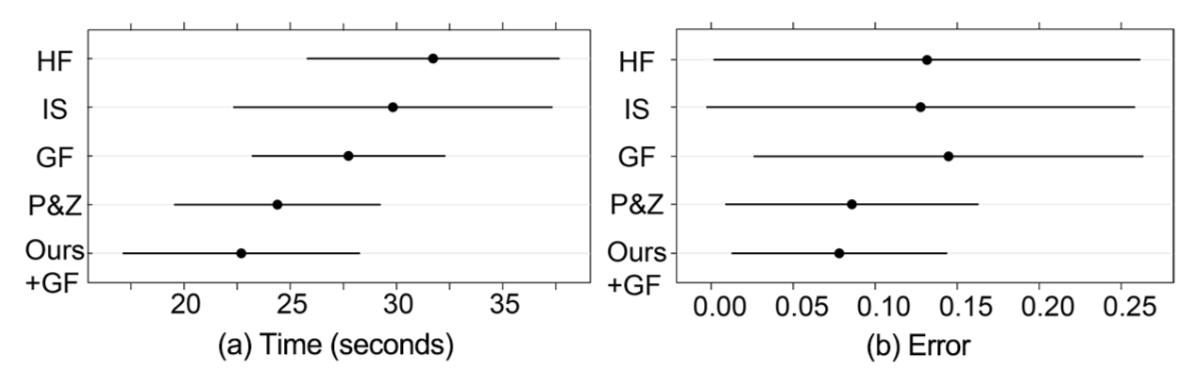
分析：每个人物都记录了完成时间和错误（用户记录的最短路径长度与真实最短路径长度之间的误差），每个人每种技术进行了3次，故而可以计算平均时间和错误。

结果：根据图所示，在时间方面，Ours+GF会比其他所有技术都更快，这支持了假设1，但只是部分支持假设2，毕竟Ours+GF和P&Z之间有大幅重叠。而在误差方面，有大规模的置信区间，也就说明了结果并不明确。尽管这样，Ours+GF的平均值还是最低的。

讨论

Hyperbolic vs. Pan&Zoom：被试提到：“双曲线鱼眼会导致挤压跟变形，有些边甚至会有很大的曲率，而平移缩放则保持了一个稳定的布局以便进行路径探索，尽管丢失了一部分上下文”。

iSphere：虽然iSphere文章本身说明了该技术比其他的技术在路径探索任务上更好，但是本文却只显示了这个技术略微比HF要好，却比其他的技术要差。被试提到，“iShpere在放大的时候，容易丢失一些远离的节点”，因为iShpere只渲染了焦点区域内的节点。有一些被试则没有感知到iSpher带来的畸变，这让他们觉得iShpere的交互像是在旋转一个球体，就跟平移缩放一样。

Graphical fisheye：相比于HF和IS，GF用了直线边，因此更短时间就完成了任务，然而GF的畸变导致了整体结构的破坏，于是它的错误率是最高的。被试提到：“GF的交互不够直观，而且它的畸变也是相对无法理解”

Our fisheye：虽然文章的方法基于GF，然而却得到了最好的表现。被试提到：“这个结构相关的鱼眼结合了双曲线和缩放平移的优点，直线边则有助于进行路径探索，而且即便会比较小，并且它的交互会显得更快，因为点击一个节点会放大感兴趣全区域而不用进行缩放平移”。

案例研究

探索ego-network

用了ego-facebook的数据集，4039个用户，88234条关系，已聚类为16个聚类。压力模型进行布局，引入了聚类不重叠的限制。但是边跟节点仍然非常密集，使得很难比较相互远离的节点。可以见到，光是利用传统的polyfocal的鱼眼，会产生很高的畸变，第四张图b。而本文的方法则可以避免这些问题，如图c，可以见到两个来自不同聚类的节点备选了出来，这两个节点都和本聚类有一些连接，也跟红色、粉色聚类紧密相关。图d则表明一些青色的异常节点跟红色聚类之间紧密连接。

美国主要城市的探索

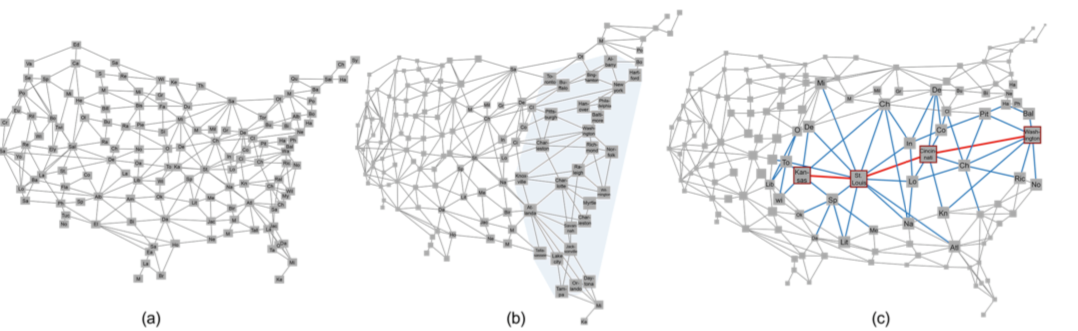
image-20181116171419003

134个节点代表美国城市，338边则表达了城市之间是相邻的关系。图b利用了聚类透镜，放大了淡蓝色区域。于是节点之间的重叠降低，可以看清这些节点的label。

而为了寻找华盛顿DC和堪萨斯之间的最短路径，路径透镜则能够放大最短路径周围的区域，良好的展示两个城市之间的关系。

在上面两个案例研究中，关于结构限制、可读性限制以及时序一致性限制都已经包含在所有的case study里面了。而关于时序一致性可以看视频。

七、总结跟未来工作

因为本文的工作都是基于节点的二维坐标系，而不是图结构。那么一些跟焦点节点相关的子结构展示的不是很清晰，特别是有些节点跟这个节点之间的欧氏距离比较大。并且作者期望将该方法用于地图，3D面片之类的。