dyngraph2vec:Capturing Network Dynamics using Dynamic Graph Representation Learning
- 论文原文:dyngraph2vec: Capturing Network Dynamics using Dynamic Graph Representation Learning
- 作者:Goyal, Palash, Sujit Rokka Chhetri, and Arquimedes Canedo
- 发表刊物/会议: arXiv
方法
问题陈述
- 图:$G(V, E)$
- 动态图:$\mathcal{G}={G_1,…,G_T}$
- 目标:将一个节点,通过学习一个映射方法:$f_t=\lbrace V_1,…,V_t,E_1,…,E_t\rbrace \to \Bbb{R}^d$转换为一组低维向量:$y_{v_1},…,y_{v_t}$,其中$y_{v_i}=f_i(V_1,…,V_i,E_1,…,Ei)$,是一个d维的向量,捕获了$1-i$时刻的图动态变换。
dyngraph2vec
dyngraph2vec是一个深度学习模型,输入前面几个时间片段的图,即可输出下一个时刻的图。
模型通过优化下面这个损失函数,来学习时刻$t$的图嵌入(network embedding,即其向量表达)。
$$
\begin{aligned}
L_{t+1} &= \parallel (\hat{A_{t+l+1}}-A_{t+l+1})\odot \mathcal{B} \parallel^2_F \\
&= \parallel (f(A_t,…,A_{t+l}) - A_{t+l+1}) \odot \mathcal{B}\parallel ^2_F
\end{aligned}
$$
其中,A表示图的邻接矩阵,$f$函数用来计算$\hat{A}$,也就是对$t+l+1$时刻的图的邻接矩阵的估计。
$\mathcal{B}$是惩罚项,$\mathcal{B}_{ij}=\beta, for (i,j) \in E_{t+l+1}, else 1$。
$\odot$表示一种矩阵的布尔运算,具体定义可以在这个pdf里面找一下(https://www.math.fsu.edu/~pkirby/mad2104/SlideShow/s5_4.pdf),不再详述。
文章使用的深度学习模型有如下三种:$dyngraph2vecAE, dyngraph2vecRNN, dyngraph2vecAERNN$。
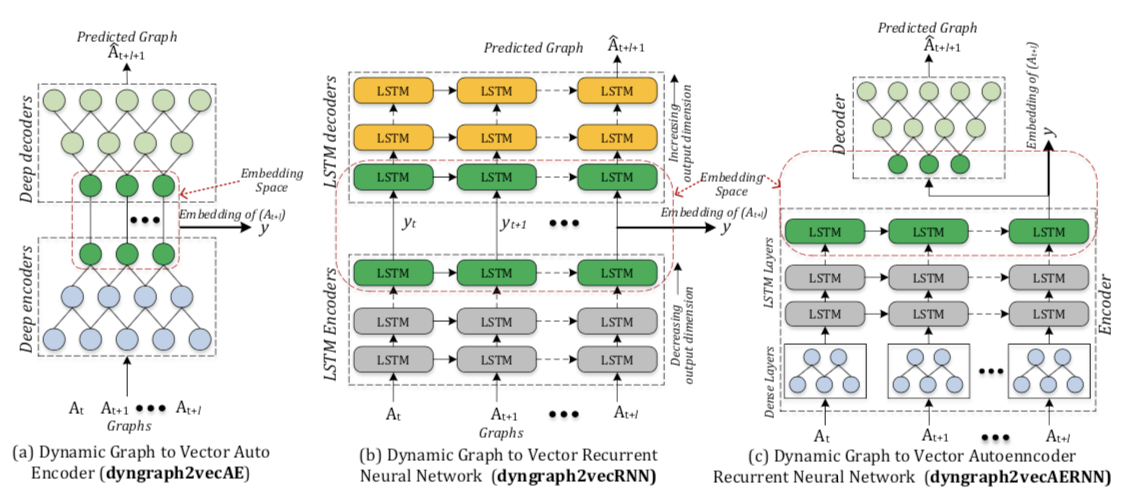
我们可以看到,这三种方法都分成两个步骤,Deep encoders的目的,是输入动态的邻接矩阵,为每个节点生成低维向量;Deep decoders则可以根据低维向量,来生成下一时刻的预测图。